How to Count to 31 on One Hand

I was reading The Unbeatable Squirrel Girl, a really funny and clever comic from a while back, and it reminded me of a cute, but also really cool trick, for counting on one hand.

Imagine from pinky to thumb, that the value of each finger doubles:

  Pinky = 1
  Ring = 2
  Middle = 4
  Index = 8
  Thumb = 16

And each finger can be either Up/On (1), or Down/Off (0).

So let's start counting. I show it as multiplication and addition here, as vectors, but you can just hold up your hand, or lay it on a surface like a keyboard or piano, whatever makes sense for you, and just feel it on your fingers.

1: 1(1) + 2(0) + 4(0) + 8(0) + 16(0) = 1 + 0 + 0 + 0 + 0 = 1
2: 1(0) + 2(1) + 4(0) + 8(0) + 16(0) = 0 + 2 + 0 + 0 + 0 = 2 

Simple enough so far. You can see from the ones and zeroes, it's just the position of your fingers. But what about 3, a number that you don't have a finger for? Just set your pinky and ring finger both to the ON position.

3: 1(1) + 2(1) + 4(0) + 8(0) + 16(0) = 1 + 2 + 0 + 0 + 0 = 3

And numbers larger than what we have fingers for, like 17? Pinky and thumb are ON, the rest are OFF.

17: 1(1) + 2(0) + 4(0) + 8(0) + 16(1) = 1 + 0 + 0 + 16 = 17

Normally when we think of numbers, we think of Arabic Numerals in Base 10, meaning 0 through 9, with 10, 20, 30, ..., 100, etc., as like the next iteration.

When we use this approach, we're counting in Base 2, also known as Binary. If we think of our fingers each as representing binary states, we can infer the value just from 0's and 1's. But, understanding the relationship between Base 10 and Base 2 visually and kinesthetically through our fingers makes it easier to understand.

In other words, starting from 0, we can think of each finger as representing 2** (to the power of) the incrementing values of our fingers:

  1: 2**0 == Pinky
  2: 2**1 == Ring
  4: 2**2 == Middle
  8: 2**3 == Index
  16: 2**4 == Thumb

So instead of:

17: 1(1) + 2(0) + 4(0) + 8(0) + 16(1) = 1 + 0 + 0 + 16 = 17

We can just represent it as:

17: 1 0 0 0 1

As I was reading the comic, I couldn't help but start counting from 0 to 31, it was just fun to do, even meditative. It took a bit of effort at first, but now I can usually on two hands get to 128 fairly trivially. Going from 128 to 256 I usually end up losing focus or making a mistake somewhere along the way, but it's still really fun!

Here is our full table:

  n:   1 2 4 8 16
  0:   0 0 0 0 0
  1:   1 0 0 0 0
  2:   0 1 0 0 0
  3:   1 1 0 0 0
  4:   0 0 1 0 0
  5:   1 0 1 0 0
  6:   0 1 1 0 0
  7:   1 1 1 0 0
  8:   0 0 0 1 0
  9:   1 0 0 1 0
  10:  0 1 0 1 0
  11:  1 1 0 1 0
  12:  0 0 1 1 0
  13:  1 0 1 1 0
  14:  0 1 1 1 0
  15:  1 1 1 1 0
  16:  0 0 0 0 1
  17:  1 0 0 0 1
  18:  0 1 0 0 1
  19:  1 1 0 0 1
  20:  0 0 1 0 1
  21:  1 0 1 0 1
  22:  0 1 1 0 1
  23:  1 1 1 0 1
  24:  0 0 0 1 1
  25:  1 0 0 1 1
  26:  0 1 0 1 1
  27:  1 1 0 1 1
  28:  0 0 1 1 1
  29:  1 0 1 1 1
  30:  0 1 1 1 1
  31:  1 1 1 1 1

Or, on our hands:

First image I found on google images. They went the opposite direction (thumb -> pinky) rather than what I said but it amounts to the same thing. You can also reverse the up and down if your pinky is capable of that, and then you get cool ninja / spiderman / punkrock handsigns. Whatever works for you, have fun with it.

During my Insight Fellowship after leaving academia, I struggled to learn a lot of the algorithmic and other computer science and software engineering fundamentals that I needed for industry. I didn't have the training and it definitely didn't come to me intuitively. Another Fellow in the group who had a much deeper intuition towards algorithms would often help me study, and one of the algorithms he worked through with me was in converting a decimal (number) to a binary representation. Rather than counting on my hands (honestly that may have been better...), I came to understand the algorithm as a vector representation, just another way of getting at the same thing, but either way, in so doing, a lot of things clicked into place for me. Not just how to write algorithms, but how to understand mathematical relationships, and in understanding aspects of natural philosophy, or how the universe works.

Imagine a World where people counted this way. What kind of culture would this be? What would be their myths, laws, philosophies, arts, and sciences?

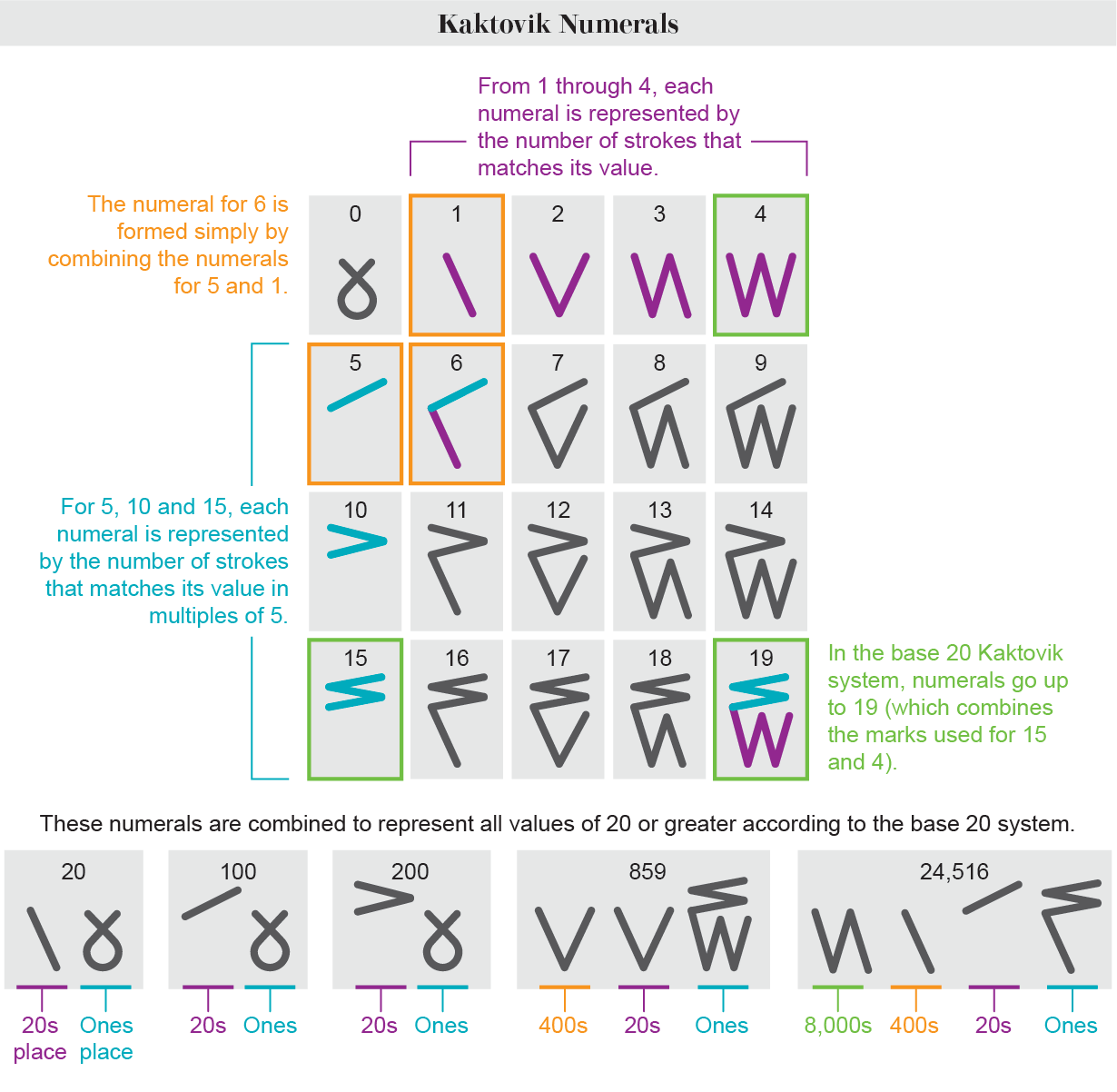
There are other ways to reconceptualize numbers physically. This system is in Base 20, and computations can be inferred from the physical relationship between strokes:

A Number System Invented by Inuit Schoolchildren

Imagine a world where people counted this way? You don't have to imagine it.

From the article linked above:

The Alaskan Inuit language, known as Iñupiaq, uses an oral counting system built around the human body. Quantities are first described in groups of five, 10, and 15 and then in sets of 20. The system “is really the count of your hands and the count of your toes,”...

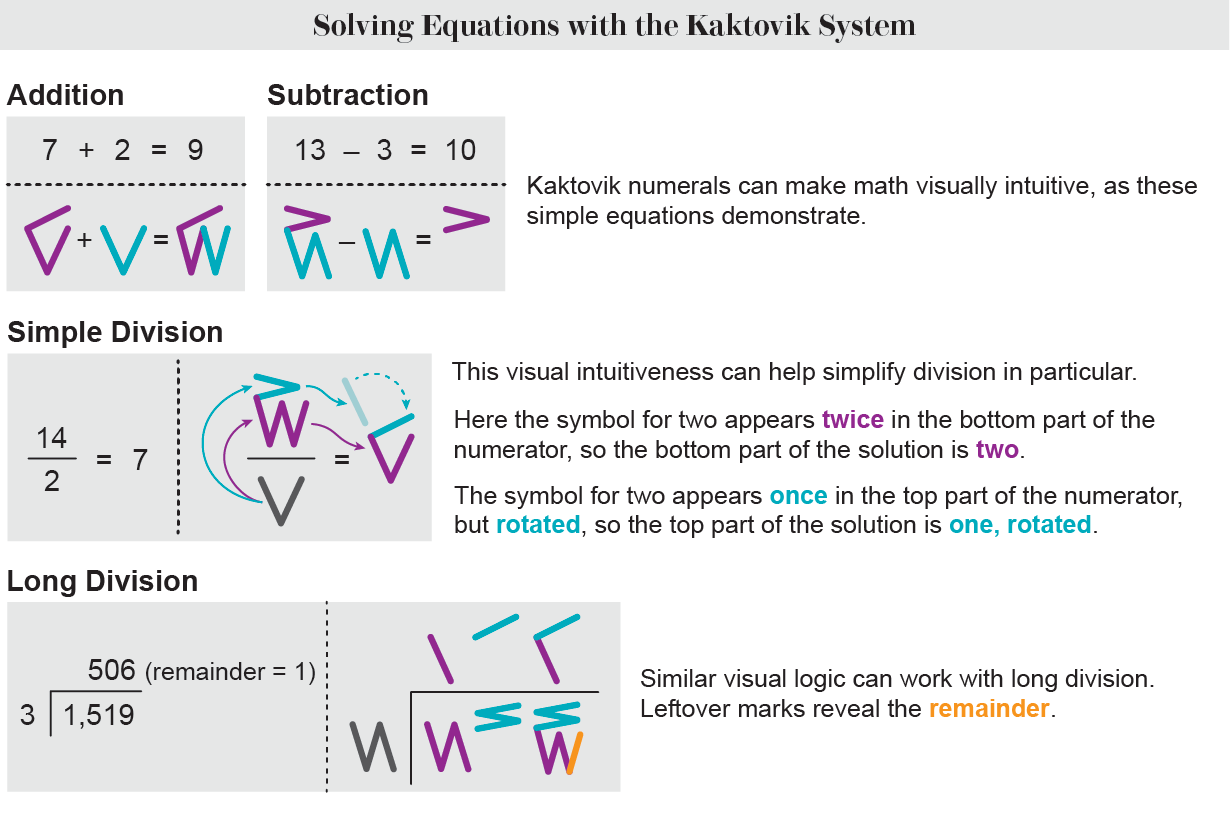
Because of the tally-inspired design, arithmetic using the Kaktovik numerals is strikingly visual. Addition, subtraction and even long division become almost geometric. The Hindu-Arabic digits are an awkward system, Bartley says, but “the students found, with their numerals, they could solve problems a better way, a faster way.”...

Thanks to efforts by linguists working with the Script Encoding Initiative at the University of California, Berkeley, the numerals were included in the September 2022 update of Unicode, an international information technology standard that enables the digitization of the world’s written languages. The new release, Unicode 15.0, provides a virtual identifier for each Kaktovik numeral so developers can incorporate them into digital displays. “It really is revolutionary for us,” Judkins says. “Right now we either have to use photos of the numerals or write them by hand.”

As of Unicode 15.0, you can even use these symbols in your digital communications, as cited in the same article above:

Credit: Amanda Montañez; Source: “Unicode Request for Kaktovik Numerals,” by Eduardo Marín Silva and Catherine Strand. Submitted to Unicode Technical Committee Document Registry March 16, 2021 (reference)